What is Lumped Heat Transfer Analysis ?
LUMPED HEAT ANALYSIS
Aricle written By : Pramod Yadav
Heat transfer from a solid to a liquid involves two phases of heat transfer :
- Conduction of heat from interior of solid body to its surface
- Convection of heat from surface to liquid medium through convection.
The conduction from inside the body to the surface gets its driving force from the temperature gradient between the interior of the solid body ( which may be generating heat internally) and the outer surface of the body . The internal heat transfer across the body stops once the temperature throughout the body becomes the same, or in other words, the temperature gradient is zero.
Also Read : Heat Exchanger Design
Mathematically,
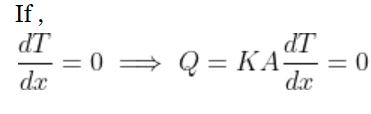
The rate of heat transfer inside the body depends upon the internal resistance which in turn depends upon the conductivity (K) and the size of the body concerned.
If the size of body or radius of body ( in case of sphere or cylinder) is too small or conductivity of the body is too high, resulting in a negligible amount of resistance, it will take very small amount of time or almost negligible time to transfer heat throughout the body and ultimately achieving thermal equilibrium.
Also Read : What is Pump Head and Shut-off Head ?
Such a case where internal resistance of the body is almost negligible, the heat transfer throughout the body will be instantaneous and thermal equilibrium inside the body will be achieved in no time resulting in the body having the uniform temperature throughout the body.
Therefore, it can be concluded that a body in which temperature is not a function of position inside a body but only a function of time is known as “Lumped Heat Capacity Analysis”.
Note : Internal heating resistance cannot be zero and rate of heat transfer cannot be infinite , so it will always take time to reach thermal equilibrium. Therefore,there cannot be a perfect Lump Heat Capacity System but a good approximation to it can be assumed.
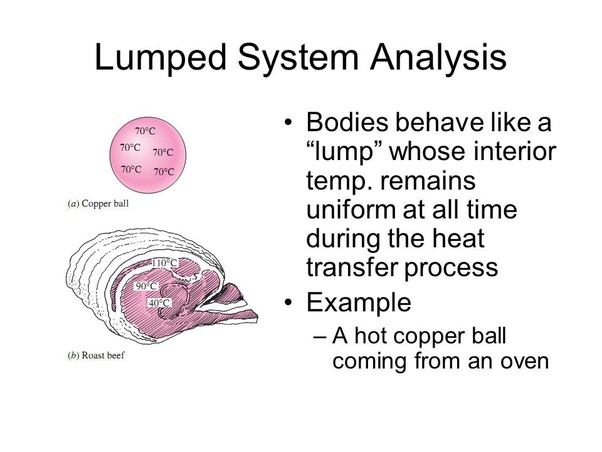
Example : A copper ball taken out of an oven , due to its small size and high thermal conductivity , will have high heat transfer rate and will result in uniform temperature throughout the ball and making it an ideal condition for approximation to Lumped Heat Analysis whereas a roasted beef due to lower thermal conductivity will have lower heat transfer rate and a variation in temperature throughout the body.
Lumped Heat Analysis Calculation for a hot ball exposed in air :
When a copper ball is taken out of hot water or the oven in air , it can be approximated to the Lump Heat Capacity system.
Heat transfer from the surface of the ball to the outside surrounding through the convection process will decrease the accumulation of heat inside the body.
Also Read : Design of Cooling Tower
Ignoring conduction inside the body due to Lump Heat Capacity system,
By heat balance at the surface of ball ,
Heat released to air by convection = Change in Internal Heat Accumulation in body
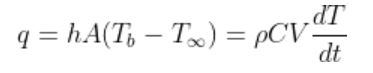
Where,
h is heat transfer coefficient,
A, heat transfer area (Surface Area)
C, the specific heat capacity of ball,
V , the volume of ball,

When will Lumped Heat Analysis be applicable to a system ?
The Lumped Heat analysis will be reasonably applicable when the result from the approximation remain within an error of 5 %.
To analyze whether a system is applicable to Lumped Heat Analysis , the value of a dimensionless number “Biot Number” is considered.
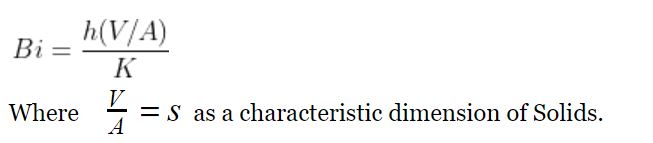
Biot’s number is the ratio of internal resistance ( Conduction) to the external resistance (convection) during heat transfer from a body to surrounding.
As Lumped Heat Analysis assumes a uniform temperature throughout the body, the conduction resistance will be zero, which means Biot Number is zero.
So, it can be said that,
For perfect Lumped Heat Capacity System, Bi =0.
If Biot’s Number is less than 0.1,the internal resistance will be negligible and will be a good approximation to Lumped Heat Analysis and time required for conduction will be nearly to zero.
And if Biot’s Number is greater than 20, the external resistance will be very less resulting in very fast convection but the conduction will be very slow.
ImageSource : Quora